สร้างแลนด์มาร์ค!! ชำแหละทุกแง่มุม

ไอเทมไหนดี เมืองแถบไหนเจ๋ง มาดูกัน

          ถ้าพูดถึงเกมสุดฮิตตอนนี้คงหนีไม่พ้นเกมเศรษฐีในไลน์ เพราะไม่ว่าจะหันซ้ายหันขวาไปไหนก็เจอแต่ “สร้างแลนด์มาร์ค” “ไม่นะ เมืองถูกยึดไปแล้ว” ฯลฯ ตัวผมเองก็เพิ่งมาติดเกมนี้ได้ไม่นานเช่นกัน แต่ก็ไม่รอด ติดงอมแงมไปแล้ว ฮาๆ สำหรับใครที่ยังไม่ได้เล่นเกมนี้ ทดลองเข้าไปโหลดกันได้ใน App Store นะครับ ชื่อ LINE Let’s get rich ครับ

          รูปแบบการเล่นเกมนี้ก็คล้ายๆ กับเกมเศรษฐีทั่วๆ ไปที่เคยเล่นมาตั้งแต่เด็ก เพียงแต่เพิ่มดีกรีความน่ารักโมเอ้เข้าไป รวมไปถึงไอเทมพิเศษแบบต่างๆ ที่อนุญาตให้เราจ่ายเงินในเกมซื้อไว้ก่อนจะเล่นเกม

          และด้วยความที่เป็นคนชอบหาเรื่องใส่ตัว จะให้เล่นเฉยๆ มันก็กระไรอยู่ อย่ากระนั้นเลยมานั่งขบคิดปัญหาที่เกิดสงสัยขึ้นมาระหว่างการเล่นเกมดีกว่า!

          tag ห้องมาบุญครอง เพราะเป็น Mobile App นะครับ รวมไปถึงห้องซิลิคอนวัลเลย์ก็เช่นกัน

          tag หว้ากอ เพราะมีการคำนวนทางคณิตศาสตร์ ทั้งความน่าจะเป็น และเรื่อง Markov Chain นะครับ น่าจะพอมีประโยชน์กับท่านใดที่กำลังเรียนอยู่

 

ไอเทมปาลูกเต๋าได้ double ดีจริงไหม?

          หนึ่งในคำถามที่หลายๆ คนคงถกเถียงกันว่าจ่ายเงินเพิ่มเพื่อให้ปา double ได้ในตาแรกดีจริงหรือไม่ เพราะบางทีดวงซวยๆ ก็ปาแล้วเข้าเกาะร้างบ่อยๆ ก็มี บางทีซวยโคตรๆ ปาไปโดนเกมเสี่ยงดวง แถมเล่นแพ้ แล้วต่อด้วยเข้าเกาะร้างอีกต่างหาก

          คำถามนี้ผมขอแยกออกเป็นสองคำถามย่อยนะครับ

          ระหว่างใช้ไอเทมกับไม่ใช้ไอเทม แบบไหนจะมีโอกาสเข้าเกาะร้างสูงกว่ากัน? และ แบบไหนจะเดินได้ไกลกว่ากัน?

          เพื่อความง่ายต่อการคำนวน และไม่ให้กระทู้ชวนปวดหัวเกินไปนัก ขอคำนวนถึงเฉพาะกรณีที่ตกช่องเกาะร้างภายในการทอยลูกเต๋าสองครั้งติดนะครับ

          ก่อนอื่นมาดูกรณีที่ไม่ใช้ไอเทมกันก่อนนะครับ ถ้าเราวาดกราฟความน่าจะเป็นออกมา ก็จะได้หน้าตากราฟราวๆ นี้

 

 

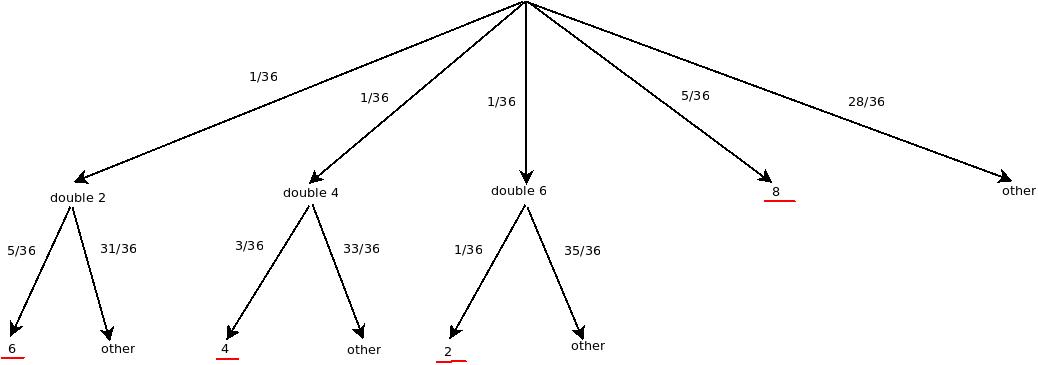
          (สำหรับน้องๆ คนไหนที่เรียนวิชาความน่าจะเป็น การเขียนกราฟแบบนี้จะช่วยให้คำนวนได้ง่ายมากขึ้นครับ โดยเฉพาะถ้าคำนวน Conditional Probability)

          ตรงนี้เราจะสนใจเฉพาะกิ่งที่ผมขีดเส้นแดงไว้นะครับ (เดินไป 8 ช่องพอดี) เราจะนำตัวเลขความน่าจะเป็นที่กำกับไว้บนกิ่งมาคำนวนเพื่อหาโอกาสที่จะติดเกาะร้าง (X) กัน

 

 

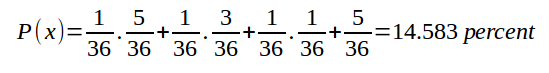
          จากนั้นเราก็ทำการคำนวนแบบเดิมกับกรณีที่เราซื้อไอเทมมาด้วย กราฟที่ได้ก็จะหน้าตาคล้ายๆ เดิม แต่เพราะเราใช้ไอเทมที่ทำให้ทอยได้ double อย่างแน่นอน ผลลัพธ์ที่ออกมาย่อมมีเพียง 6 ทางเท่านั้น (1-1, 2-2, 3-3, 4-4, 5-5, 6-6) ครับ เป็นที่มาของความน่าจะเป็นของกิ่งแรกที่เท่ากับ 1/6

 

 

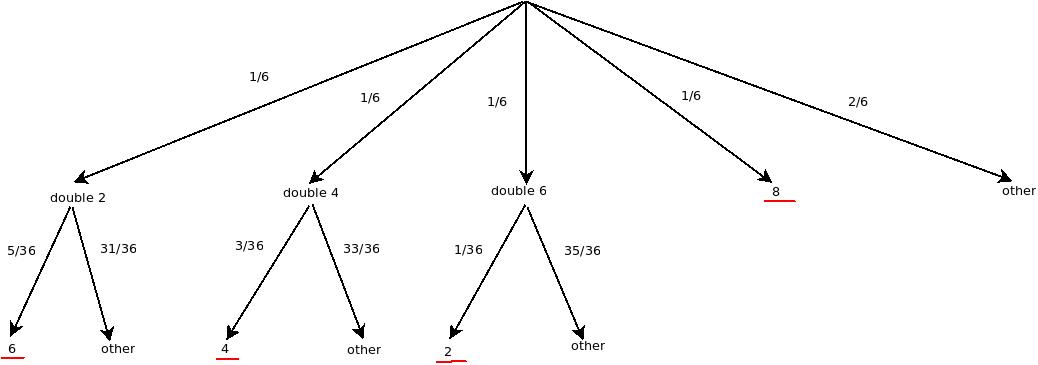
          และความน่าจะเป็นที่จะทอยได้ 8 ช่อง

 

 

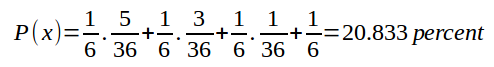
          เป็นที่เห็นได้อย่างชัดเจนว่าการใช้ไอเทมทำให้เราเสี่ยงต่อการติดเกาะร้างสูงกว่ามาก

          แต่เราจะพิจารณาจากตัวเลขความน่าจะเป็นอย่างเดียวไม่ได้ เพราะการใช้ไอเทมก็ส่งผลให้เรามีโอกาสได้เดินไปไกลกว่าคนอื่น ซึ่งทำให้เราได้เปรียบในการเล่นเกมด้วย คำถามถัดมาก็คือ ความเสี่ยงที่เพิ่มขึ้นมานี้คุ้มหรือไม่กับระยะทางที่น่าจะได้เพิ่มขึ้น ซึ่งก่อนที่จะตอบคำถามนี้ได้ เราก็ต้องตอบอีกคำถามหนึ่งที่ยังเหลืออยู่เสียก่อน – เราจะทอยไปได้ราวๆ กี่ช่อง?

          สมมติให้ E[X] เป็น Expected Value ของการทอยลูกเต๋าสองครั้งซึ่งมีค่าเท่ากับ 7 เราจะสามารถหากรณีที่ไม่ได้ใช้ไอเทมว่ามี Expected Value ของจำนวนช่องที่จะเดินได้เท่าไรโดย

          (1/36)(2+E[X])+(1/36)(4+E[X])+(1/36)(6+E[X]) + (1/36)(10+E[X]) + …. + (2/36)*3 + (2/36)*4 + (4/36)*5 + …

          นั่นคือเราจำแนกโอกาสที่จะทอยได้ double พร้อมกับจำนวนช่องที่เดินได้และ Expected Value ของการทอยลูกเต๋าอีกครั้ง แล้วนำมาบวกกับจำนวนเลขคูณกับโอกาสที่ยังเหลืออยู่

          เมื่อนั่งกดเครื่องคิดเลขแล้ว ก็จะได้ออกมาว่า ค่าเฉลี่ยคาดหวังของการทอยลูกเต๋าสองครั้งแบบไม่ได้ใช้ไอเทมอยู่ที่ 7.972 ช่อง

          ในทางกลับกัน ถ้าเราใช้ไอเทมทอยได้ double ค่าเฉลี่ยคาดหวังก็จะกลายเป็น

          (1/6)*8 + (1/6)(2+E[X]) + (1/6)(4+E[X]) + … = 12.833 ช่อง

          ต่อไปก็คือคำถามสุดท้ายในหัวข้อนี้ที่ว่า จำนวนช่องที่เดินได้โดยเฉลี่ยที่เพิ่มขึ้นมานั้น คุ้มค่ากับความเสี่ยงที่เพิ่มขึ้นหรือไม่ งานนี้ผมขอดึงเอาสูตร Sharpe Ratio จากฝั่ง finance มาดัดแปลงนะครับ โดยจะทำการคำนวนจำนวนช่องที่เดินได้ต่อหนึ่งหน่วยความเสี่ยง (ในที่นี้คือโอกาสที่จะเดินติดเกาะร้าง)

          ไม่ใช้ไอเทม = 7.972/14.583 = 0.547 ช่องต่อ percent

          ใช้ไอเทม = 12.833/20.833 = 0.616 ช่องต่อ percent

          ดังนั้นจะเห็นได้ว่า ถ้าเราใช้ไอเทมจะเดินได้จำนวนช่องมากกว่าต่อหนึ่งหน่วยความเสี่ยง เพราะฉะนั้นผมคิดว่าไอเทมนี้คุ้มค่าอยู่ครับ

 

สุ่มเลือกลำดับการเดินเป็นคนที่เท่าไรดี

          เวลาที่เล่นเกมเศรษฐี ตัวเกมจะแสดงไพ่ตามจำนวนคนเล่นให้ผู้เล่นแต่ละคนเลือกว่าจะได้เดินเป็นลำดับที่เท่าไร คำถามก็คือ เราควรจะเลือกเป็นคนที่เท่าไรดี เลือกเป็นคนแรกเลยดีมั้ย หรือจะให้คนอื่นๆ ได้เลือกไปก่อน?

          คำถามนี้สามารถโมเดลออกมาเป็น Stochastic Tree ได้เหมือนกับที่ทำกับคำถามก่อนๆ แต่ผลที่ได้ไม่ค่อยน่าสนใจนัก ผมจึงขอรวบรัดตัดความไปเลยว่า โอกาสที่ท่านจะได้เล่นเป็นลำดับ 1 หรือ 2 นั้นไม่ขึ้นอยู่กับอันดับการเลือกไพ่ ไม่ว่าท่านจะเลือกไพ่เป็นอันดับที่เท่าไร ก็มีโอกาสได้ลำดับการเล่นต่างๆ เท่ากันเสมอ และเรื่องนี้เป็นจริงไม่ว่าจะเล่นในโหมด 3 คน หรือ 4 คนก็ตาม

 

เมืองแถวไหนคนตกบ่อยสุด

          คำถามนี้ถามง่ายแต่ตอบยาก ปัจจัยที่ส่งผลให้คนตกตำแหน่งต่างๆ ในเกมนี้หลักๆ มีสองอย่างคือ การทอยลูกเต๋า (ตามปกติมักจะทอยได้ราวๆ 7 ช่อง) และการ์ดพิเศษต่างๆ ที่คอยเด้งผู้เล่นไปตามตำแหน่งต่างๆ บนกระดาน เท่าที่ผมเช็คมามีการ์ดพิเศษทั้งหมดราวๆ 20 แบบ และในจำนวนดังกล่าวมีการ์ดที่เด้งผู้เล่นไปตำแหน่งอื่นๆ อยู่ทั้งหมด 5 ใบ แต่จากความรู้สึกในการเล่น ผมคิดว่าโอกาสที่ผู้เล่นจะโดนเด้งไปตำแหน่งต่างๆ เวลาตกช่องดวงคือราวๆ 1/3 ครับ โดยโอกาสที่จะไปแต่ละที่ (จุดเริ่มต้น, เกมเสี่ยงดวง, เกาะร้าง, เครื่องบิน และภาษี) มีโอกาสเท่าๆ กันครับ

          ขอไม่นับกรณีที่โดนเด้งเพราะทอยได้ double สามครั้งติดนะครับ เดี๋ยวจะไปกันใหญ่ อย่างไรก็ดีโอกาสจะทอยได้ double สามครั้งติดก็ค่อนข้างน้อยอยู่แล้ว ไม่มีผลต่อตัวเลขสุดท้ายเท่าไรแน่นอนครับ

          การที่จะตอบคำถามนี้ได้จำเป็นต้องโมเดลการเดินเสียก่อน เราสามารถทำได้โดยมองช่องแต่ละช่องบนกระดานเป็น state หนึ่งใน Markov Chain ยกตัวอย่างเช่น หากเราอยู่ใน state จุดเริ่มต้น เรามีโอกาส 1/36 ที่จะไปตกเกมเสี่ยงดวง, 2/36 ที่จะไปตกเมืองข้างๆ, ฯลฯ บวกกับโอกาสที่จะโดนเด้งไปตามจุดต่างๆ ด้วยการ์ดดวง และระบุให้มีโอกาสไปช่องต่างๆ เท่าๆ กัน (ยกเว้นช่องเดิม) เมื่อผู้เล่นตกช่องเครื่องบิน (ตอนแรกคิดว่าจะโมเดลให้ไปเฉพาะเมืองต่างๆ แต่บางทีผมก็บินไปเกาะร้างเพื่อถ่วงเวลา ฮาๆ)

          เมื่อเราเขียน Transition Matrix สำเร็จแล้ว เราก็พร้อมที่จะคำนวน Stationary Distribution หรือความน่าจะเป็นที่เราจะกระจายไปอยู่ในช่องต่างๆ ครับ ใครที่ขยันจะตั้งสมการแล้วแก้ก็ได้นะครับ ส่วนผมขี้เกียจ ขอใช้ R แก้ให้แล้วกัน

 

 

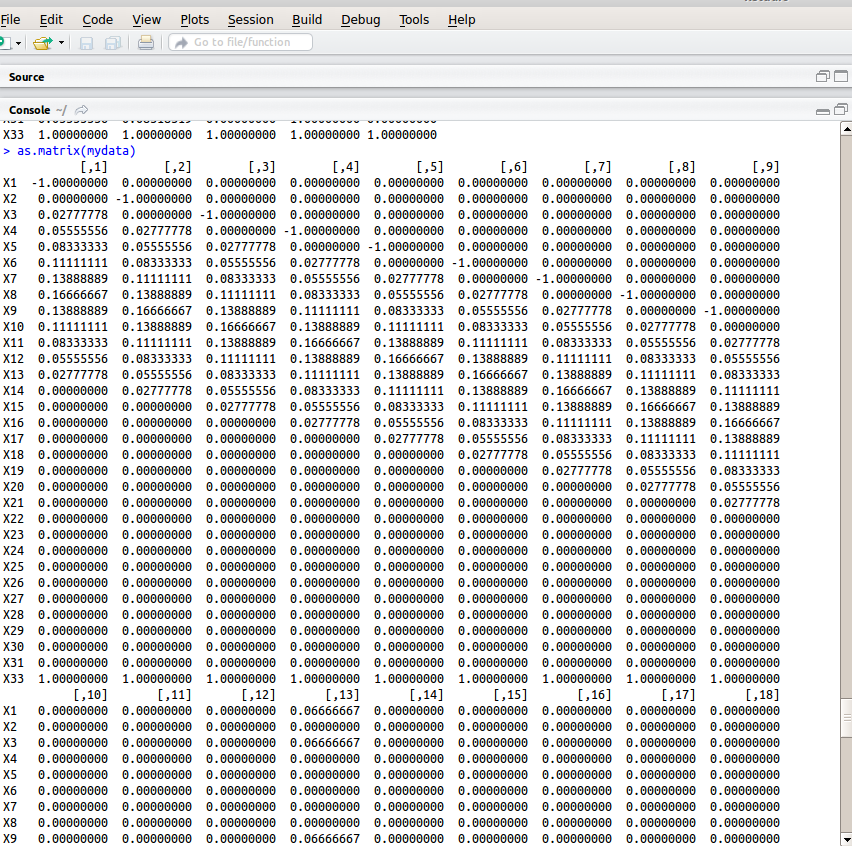
          สำหรับวิธีที่ใช้ในการ solve หา stationary distribution โดย R สามารถอ่านได้จากเอกสารนี้ครับ

http://www.stat.berkeley.edu/~mgoldman/Section0220.pdf

 

 

          เมื่อเสร็จแล้ว เราจะได้ข้อมูลดังต่อไปนี้ออกมา

          [1] 0.03286354 0.02720946 0.03366252 0.02780988 0.02886665 0.03001790 0.03012009 0.03049554 0.03688905 0.03112612
          [11] 0.03120752 0.03139146 0.03176403 0.03206402 0.03219178 0.03227182 0.03213176 0.03193141 0.03169170 0.03142884
          [21] 0.03170653 0.03192301 0.03196290 0.03196129 0.03689451 0.03188316 0.03066458 0.02947627 0.02885965 0.02818475
          [31] 0.03331648 0.02603177

          ซึ่งก็คือโอกาสที่ผู้เล่นจะไปอยู่ในช่องต่างๆ เริ่มจากจุดสตาร์ทนั่นเอง ถ้านำไปรวมกับภาพแผนที่ของเกมแล้ว ก็จะออกมาแบบนี้ครับ

 

 

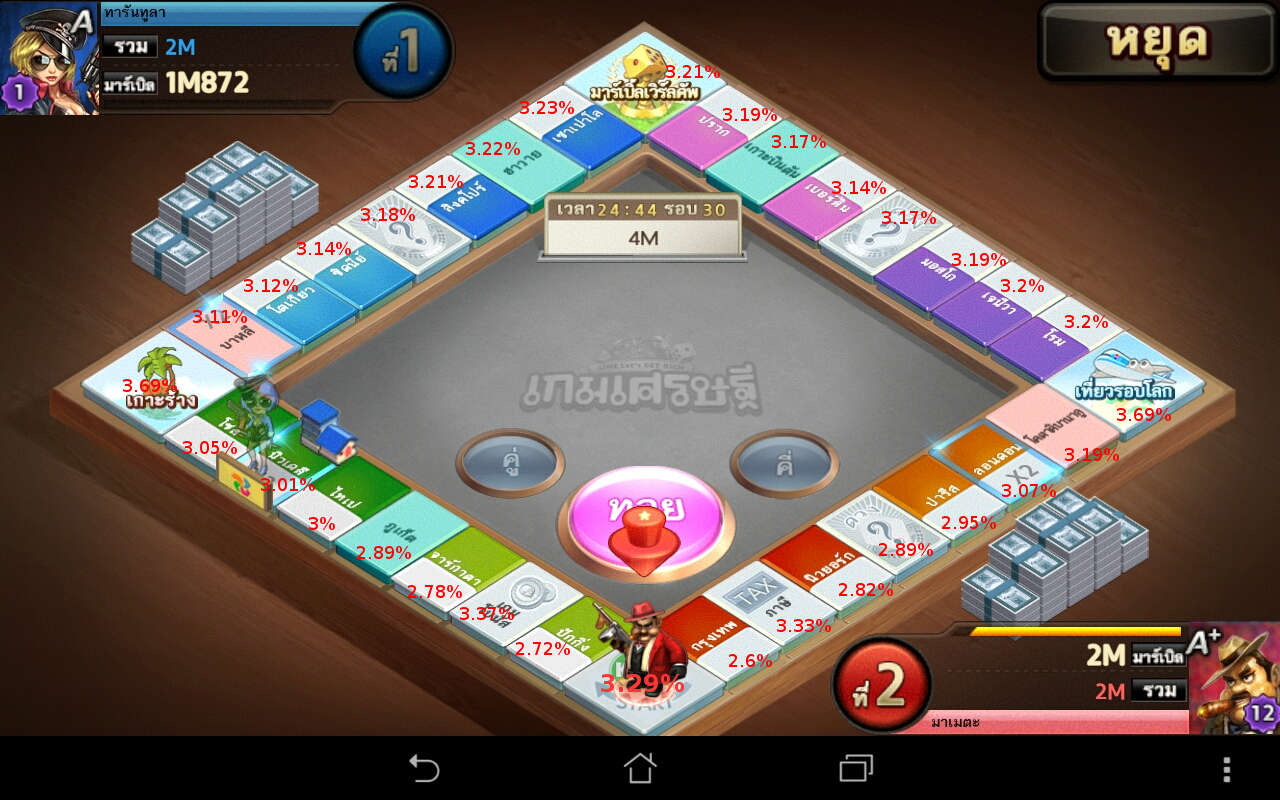
          โอกาสตกแต่ละช่องไม่ต่างกันมากนัก แต่ถ้าเป็นผม ผมคงเลือกที่จะเน้นโซนตั้งแต่โตเกียวไปจนถึงโรมครับ เพราะมีโอกาสตกสูงกว่าบริเวณอื่น รวมไปถึงมีค่าผ่านทางสูงพอที่จะทำให้ผู้เล่นล้มละลายได้ง่ายๆ ส่วนแถวปักกิ่งถึงโซลนั้นปล่อยผ่านได้ก็ปล่อยผ่านไปเลยครับ (ปกติผมซื้อไว้แค่บ้านหลังเดียว เก็บเงินไปซื้อที่อื่นดีกว่า)

          ขอจบเรื่องของเกมเศรษฐีไว้เพียงเท่านี้นะครับ ขอให้ทุกท่านโชคดีกับการทอยลูกเต๋าครับ

 

ที่มา : คุณ Charles Y. @Pantip